The Algebra Gatekeepers

How schools deny advanced math to their highest-scoring students

---

More than half of students predicted to succeed in advanced math are denied access to those classes.

Our research firm evaluates federally funded education programs in K-12 schools. In the early to mid-2000s, these grant-funded program evaluations began requiring measurable objectives and pre- and post-data comparisons. During this period, federal grants aimed at getting more low-income and minority students into advanced STEM courses became a common trend.

These program evaluation requirements led to a striking discovery. Tens of thousands of high-scoring students in North Carolina were not enrolled in advanced math courses. When staff working on the grant-funded programs (typically school counselors, school improvement teams, and administrators) discovered they already had hundreds of top-scoring, academically successful students in a single middle or high school who were not in advanced math, they usually wanted to enroll them. More often than not, they were told by their math departments that they couldn't enroll these students because students needed a teacher recommendation.

Educators involved in these grant-funded programs became curious about who was actually enrolled in advanced math and how those students had gained access. They asked us to examine the data to find out, as they had simply assumed that the students with the highest math scores were the ones in advanced math classes. Very few low-income and minority students were enrolled in advanced math, and the school counselors and administrators assumed this was because these students didn't score high on assessments. This incorrect assumption led them to write objectives for their grant-funded programs focused on increasing the number of low-income and minority students who scored high in math, believing there were virtually none. They had also incorrectly assumed that if their grant-funded services resulted in these students scoring higher that they would enroll in advanced math.

---

When academic achievement and advanced enrollment diverge

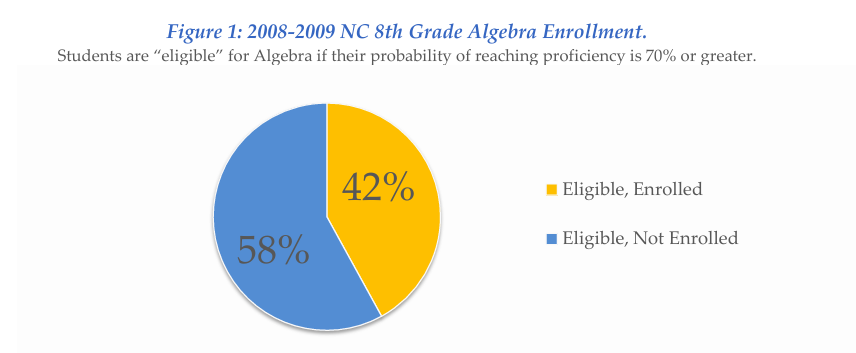
In 2009, North Carolina administrators were becoming more aware that enrollment in advanced math classes was not done by academic achievement, largely due to the new trend of federal grants aimed at increasing enrollment of low-income and minority students. The North Carolina Association of School Administrators hired us to work with SAS to investigate how math placement related to math achievement in all school districts in the state.

SAS Institute analyzed academic scores and math course enrollment patterns for all of North Carolina and for each school system. SAS Institute is a leading global provider of advanced analytics and statistical software, with over 12,000 employees and more than 80,000 customer sites in 140 countries, making it a major player in enterprise data solutions across industry and academia. Their analysis revealed the extent of these placement gaps. Among 7th graders with strong statistical predictions for success in advanced math, fewer than 50% were actually placed in 8th-grade algebra. At the same time, many students in those advanced classes had lower success predictions than students who were not recommended for the class.

This is not a small problem affecting a few students. This analysis revealed a systematic failure affecting tens of thousands of children across North Carolina alone, wasting human potential on a massive scale. The study done in 2009 showed that about 35,000 North Carolina middle school students were predicted to be successful in 8th-grade algebra but were not enrolled. They went on to take 9th-grade algebra, and more than 25,000 of them scored at the highest level on the 9th-grade algebra end-of-grade test. Yet despite this demonstrated high performance, they remained in the standard track rather than advancing to more rigorous mathematics courses, such as Honors, Advanced Placement, or IB math classes.¹

In some schools that we worked with, either evaluating their grants or helping them with their school improvement plans, principals overrode the typical placement requirement of teacher recommendations and enrolled all high-scoring students into the advanced math track. If we were working on the evaluation of a grant-funded program we would follow the students’ progress over several years. Nearly all students who were moved to the advanced math track based on their academic scores were successful in earning As or Bs in the courses and remained on the advanced track. In some schools the students stayed where they were, in standard or even remedial classes, regardless of their academic scores. The educators in those schools held onto the idea that no level of academic success should give students access to advanced math. They instead used teacher recommendations exclusively.

The enrollment process created additional barriers for students and families. When students went online to select their courses, in many school districts they could not see classes that required teacher recommendations and may not have known those courses existed. Students who requested placement in advanced classes were frequently told they could not enroll, even when they had strong academic credentials. Students had no pathway to demonstrate their readiness or earn their way into these courses through their academic performance. They had to be recommended by a teacher.

We also found that mathematics placement decisions in middle school have profound consequences for students' academic trajectories. Students who took algebra in 8th grade continued to advanced high school mathematics, while those who didn’t rarely took an advanced math class in high school. The statewide data that we analyzed with SAS showed that students who took 9th-grade Algebra were far less likely to take the most challenging and rigorous math and science classes in high school compared with equally high-scoring students who took 8th-grade Algebra. Specifically, the students who scored at the top level who took 8th grade-Algebra were three times more likely to take physics and chemistry than equally scoring students who took 9th-grade Algebra. The students who scored at the second highest level were 55 times more likely to take chemistry and physics if they took 8th-grade Algebra. This pattern held true even when students were successful and high-scoring in 9th-grade Algebra. A study in one of North Carolina's largest districts found that although honors math courses were theoretically open to students who did not take 8th-grade Algebra, very few students who had not done so enrolled in the honors courses, and none of these students took calculus.² They didn't have a written rule preventing these students from advancing, but the data showed almost no one moved to the advanced track in high school.

The scale of this issue is significant. The consequences extend beyond course-taking patterns to actual achievement. The federal grant, GEAR UP, funds school districts for seven years to implement services designed to increase the number of students in advanced math and science courses. To evaluate this grant, we had to report achievement scores and course enrollment numbers for students in 11 school districts each year. We followed a cohort of students from middle school through their first year of post-secondary education. North Carolina high schools offer Math I/Algebra 1 three different ways. One way is to slow the pace and stretch the material over two courses. Our analysis of course-taking data showed that many of the highest-scoring students were enrolled in slower-paced math courses. When we compared Math 1/Algebra standardized test scores of top-scoring mathematics students (Levels 4 or 5 on 8th-grade math standardized tests), those who took the standard course significantly outperformed those in the slower-paced course, with 82% versus 41% scoring at the college ready level.

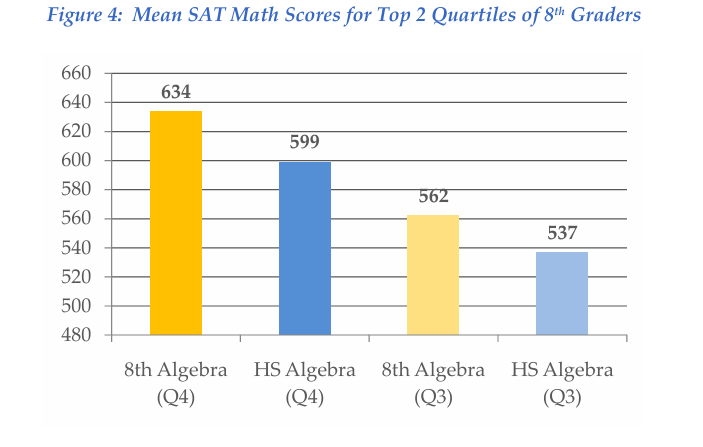
These outcomes align with earlier research showing that top-scoring students who enroll in the most rigorous version of Algebra 1/Math I score significantly higher on college entrance math assessments.³ SAS Institute conducted an analysis comparing the long-term outcomes of students who took 8th-grade algebra versus those who waited until high school. The following figure shows SAT math scores for students in the top two quartiles.⁴ The results demonstrate that even among the highest-achieving students, those who took 8th-grade algebra significantly outperformed their equally capable peers who delayed algebra until high school, with score differences ranging from 25 to 35 points.

The broader implications are troubling. Although North Carolina requires students to earn credits in four math classes that meet minimum requirements for UNC system colleges and community college pathways, the majority of students not in advanced math tracks graduate unprepared for post-secondary mathematics. In 2014, about 60% of students graduating from GEAR UP high schools did not meet the Minimum Admission Requirements for the University of North Carolina System or Multiple Measures Requirements for the North Carolina Community College System. In 2017, nearly 72% of all North Carolina juniors failed to score the ACT college-ready benchmark in math. Of students who graduated from high school in 2013 and immediately enrolled in a North Carolina community college, 52% were required to take up to 10 remedial math modules that covered arithmetic and beginning algebra.⁵

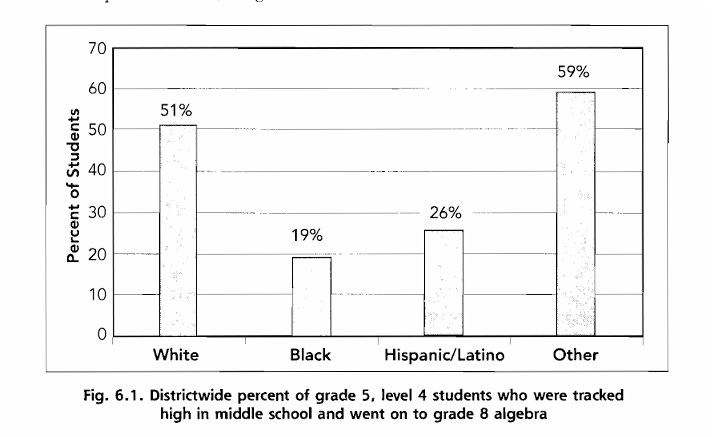
We were working with one of North Carolina's largest school districts that had several grants and school improvement plans with the objective of getting more students into top math tracks, and they discovered they didn't know what actually got a student into these tracks. They had previously assumed everything was working as it should until they had these grants, and consequently saw the data. They asked us to review their data on math tracking and help them learn what was going on. We found that the percentage of students who scored at the highest level in 7th-grade math and then were enrolled in 8th grade algebra varied dramatically by school in this district, ranging from 3% to 80%. We also found that 6th-grade placement determined both 7th and 8th-grade math course placement. Only students who took advanced 6th-grade math took pre-algebra in seventh grade, and only students from those classes took 8th-grade algebra.

Further investigation revealed that 5th grade teachers were making placement decisions before test scores were available, but the recommendation forms included test scores as if decisions were based on them. They had us survey and interview the 5th grade teachers and ask how they made placement decisions. When we asked teachers what their score predictions were based on, most said "gut feelings." Their placement rationales varied wildly. Some avoided placing students in advanced math because they "hated math" and didn't want to "torture" students. Others placed high-scoring students in standard tracks for "better foundations." Some placed high-scoring minority students in standard math because they believed research showed minorities would struggle in advanced classes.

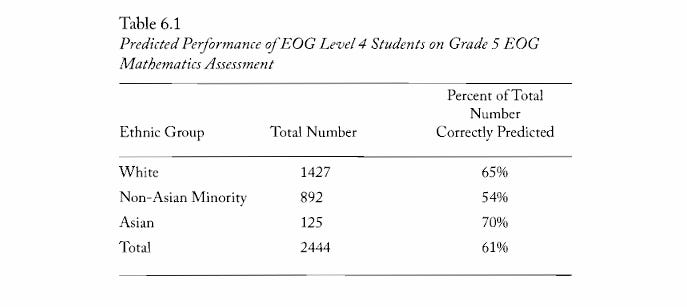
We compared teachers' predicted scores to actual test results once they were available and found systematic bias. We published these findings showing that teachers correctly predicted performance for only 60% of students, with prediction errors "not equally correct across ethnic groups."⁶

Here are results of this research published in this paper. At this time, Level 4 was the highest level on the math standardized tests.

This district had seven middle schools that received a federal grant to teach all 6th-grade math classes the way they traditionally only taught their advanced 6th-grade math, including conceptual understanding in addition to learning how to compute. The fifth-grade teachers had made recommendations, which were ignored due to this new program. When students completed this rigorous math course, sixth-grade teachers recommended 15% more students for advanced tracks than fifth-grade teachers had. Seeing students actually perform in challenging mathematics changed teachers' perceptions. However, although teachers recommended more students for pre-algebra, there were not more students who went on to take 8th grade algebra. We were evaluating this grant-funded program. It seemed to be successful, yet it didn’t lead to more students in 8th-grade algebra, even though they had more high scoring students. When we asked why more students didn’t enroll in algebra, they said this was because they had a fixed number of 8th-grade algebra classes and could not accommodate more students. When we asked why they didn't add a class, they said there were not more teachers who could teach the rigorous version of algebra and they were already struggling to have enough top track high school math teachers and therefore could not bring any more to the middle school level.

One middle school we worked with had a principal who took control after he saw the data. He moved 103 6th-grade students who had been recommended by 5th grade teachers to be in standard math into advanced math instead. All but a few earned A or B grades. This was a magnet school with a bimodal population of high-income and very low-income students. The high-scoring students who had been recommended for the low track were low-income. After their success, the high-income parents pressured the principal to move these successful low-income students back into standard math. He refused. He was then moved to a different school, and the new principal moved these students back to standard math. We published this in a peer-reviewed journal.⁷

---

A national problem

The patterns we were discovering were so startling to us and to the school counselors and principals we worked with that we began to wonder if this situation was unique to North Carolina or to the specific schools in our studies. We decided to review the research literature to see if similar patterns had been documented elsewhere. We found that this was not unique at all. These inequitable placement practices had been extensively documented across the United States for decades.

McGrath and Kuriloff found that upper-middle-class parents actively worked to maintain educational advantages for their children while blocking access for others, revealing how social class perpetuated tracking inequities.⁸ The research literature showed consistent patterns spanning from the 1980s through the 2010s. In the 1980s, studies revealed that when controlling for demonstrated proficiency, non-Asian minority students had about a 50% chance of being recommended for advanced mathematics compared to white and Asian students.⁹ Research in the 1990s found that in California, Latino students scoring above the 90th percentile on standardized tests had only about a 50% chance of being placed in college preparatory classes, while Asian and white students with similar scores had more than a 90% chance.¹⁰ A study of 6,000 students found that students from wealthier families were three times more likely to be placed into algebra than low-income students of equal ability.¹¹ The 2000s brought evidence that sixth grade placement was the strongest predictor of 8th grade math placement, with race being one of the most significant social factors determining placement among equally high-scoring students.¹² Even into the 2010s, research continued to document these patterns, including a statewide North Carolina study where educators admitted using free or reduced lunch status as "academic data" to determine student placement, and when that wasn't available, relying on race to identify students with perceived barriers to learning.¹³

We worked with other schools where the principal embraced the data and moved significant numbers of high scoring students into the advanced track and they stayed there and succeeded. We were working with School Improvement Teams in NC to help them interpret their academic data and use it to meet objectives in their School Improvement Plans. Wake Forest Rolesville Middle School’s data showed more than 100 minority students with top test scores had been recommended for remedial math.

When these high-scoring students were finally placed in advanced math, many of them excelled. One student who'd been destined for the bottom track became the highest-scoring math student in the entire school. The principal, Elaine Hanzer, presented about this at the annual conference for Superintendents, and our co-founder presented these findings at a national conference for math teachers.

The No Child Left Behind era brought sophisticated data systems to schools. North Carolina purchased EVAAS (Education Value-Added Assessment System), developed by SAS Institute. EVAAS is a statistical tool that could predict with remarkable accuracy which students would succeed in advanced courses.

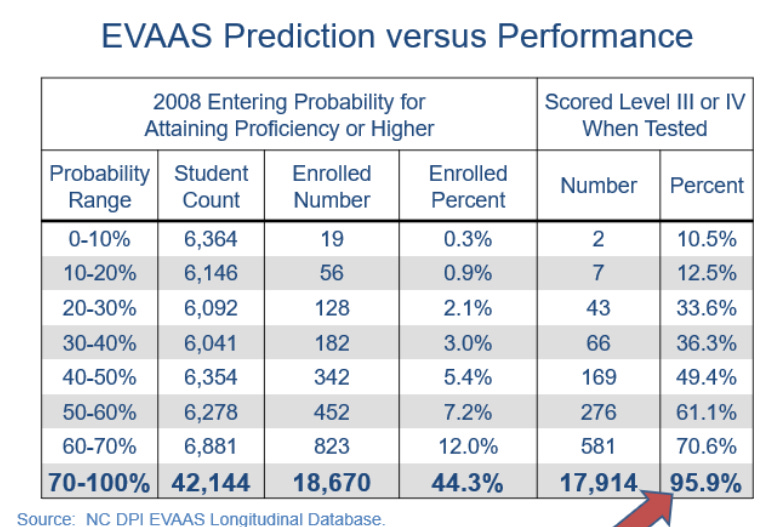
The following table provides evidence of the system's predictive validity. EVAAS uses students' prior test scores in both math and reading to calculate the probability that they will achieve proficiency (Level III or higher) on future assessments, such as 8th-grade Algebra I. These predictions assume students receive an average schooling experience for the state.

The table demonstrates a strong correlation between EVAAS predictions and actual student performance. Students were grouped into probability ranges based on their predicted likelihood of success in 8th grade Algebra I, and their actual performance was then tracked. The results show remarkable accuracy: among students with at least a 70% probability of earning Level III or higher, 95.9% actually achieved that level of performance.

The data also reveals the precision across different probability ranges. Students with lower predicted probabilities performed as expected. Those in the 0-10% range had only a 10.5% success rate, while those in the 10-20% range achieved 12.5% success. The progression is consistent, with success rates climbing steadily through each probability range. This systematic correlation between predicted and actual performance demonstrates that EVAAS provides highly reliable predictions for student achievement, making it a valuable tool for identifying students who are ready for advanced coursework.

As more and more people became aware that math placement was not done by objective criteria, and because of countless examples of principals or others not allowing more students or more qualified students into advanced math, the arbitrary nature of placement decisions became increasingly problematic. Essentially, it was up to each individual school how to make placement decisions, leading to wildly inconsistent practices across districts and schools.

---

Counted out

In 2017, the Raleigh paper News and Observer published a series of investigative reports called the "Counted Out," examining practices of labeling students as gifted in several large school districts in North Carolina. The analysis found that qualified economically disadvantaged students were less likely than their affluent peers to be placed in advanced courses, despite having similar levels of preparedness because they weren’t labeled “gifted.” (We were the source for that investigative report. At the time, we wanted to be anonymous because of all the backlash we were getting from school systems that wanted to maintain control of access to advanced courses.)

In response to mounting evidence of these inequitable practices and the resulting disparities in student opportunities, and partially in response to the "Counted Out" series, the North Carolina General Assembly took legislative action to address the issue systematically. In 2018, North Carolina passed House Bill 986, Session Law 2018-32, which included Part II: Enrollment in Advanced Mathematics Courses. This legislation established § 115C-81.36, requiring that "any student scoring a level five on the standardized test for the mathematics course in which the student was most recently enrolled shall be enrolled in the advanced course for the next mathematics course in which the student is enrolled." The law further specified that "a student in seventh grade scoring a level five on the seventh grade mathematics end-of-grade test shall be enrolled in a high school level mathematics course in 8th grade" and that "no student who qualifies under this subsection shall be removed from the advanced or high school mathematics course in which the student is enrolled unless a parent or guardian of the student provides written consent for the student to be excluded or removed from that course."

The North Carolina General Assembly asked the North Carolina Department of Public Instruction to report on the academic levels of students who were in 8th-grade algebra. The Department's report revealed that more than half the students already in advanced math classes had not scored at the highest level on standardized tests, yet no one had expressed concern about these lower scoring students being enrolled. Meanwhile, SAS’ Institute’s study showed that more than half of students who did score at the highest level were excluded from these same classes.

In the meantime, California was going through the same issue, and someone had finally achieved some success at fixing the sort for 8th-grade algebra… only to find that the students who’d gotten in based on test scores instead of teacher recommendations were simply placed back into the standard track in the ninth grade, regardless of the success they achieved in 8th-grade algebra. In 2014, CA passed additional legislation to say students who had completed 8th-grade algebra with a B or better could not be made to retake algebra in the ninth grade.

Before the North Carolina legislation, we volunteered with churches in North Carolina to help parents advocate for their high-scoring children to get them enrolled in advanced math when their teachers did not recommend them. We accompanied families to school meetings because administrators often used "data-word salad" to confuse parents, claiming that high scores and good grades somehow didn't indicate future success.

For example, we attended a meeting with the parents of a middle school girl who had earned an A in 7th-grade pre-algebra but was denied enrollment in 8th-grade algebra despite her and her parents' wishes. The teachers argued that her formative assessments didn't align with her summative performance, suggesting her previous success didn't guarantee future outcomes. The language arts teacher claimed the student had "appeared to struggle" during benchmark activities and that earning an A seemed "harder for her than for other students who achieved similar summative data results." The math teacher who had given her an A pointed to C grades on some earlier formative assessments, arguing that despite her subsequent A performance on chapter tests and other summative data points, these initial benchmark scores indicated she "sometimes struggles with foundational concepts during the formative assessment process."

The administrators nodded knowingly as teachers referenced "inconsistent performance across benchmark measures" and "concerns about the gap between formative and summative data trends." They suggested that while her final grades represented solid summative data, the formative assessment patterns revealed "areas of concern" that made advanced placement inadvisable, regardless of what the summative data actually showed about her mastery of the subject matter. This is just an example of the kind of talk the parents encountered, so the church advocacy group started bringing someone from our staff to the meetings to help them cut through this.

This type of circular reasoning, where success was reframed as evidence of potential failure, was typical of how schools justified excluding qualified students from advanced courses.

Administrators would routinely promise that students could move to advanced tracks "later, in high school," but our analyses and other research we found indicate students rarely moved to the advanced track after the eigth grade. The tracking system created rigid pathways where missing 8th-grade algebra typically meant students couldn't reach calculus by graduation, limiting their college and career options. This pattern was consistent across multiple schools we worked with, where the barrier wasn't just about having enough years to reach calculus, but about how the entire mathematics sequence was structured to funnel students into separate tracks with little opportunity for movement between them.

One fifth grader exemplified the problem. He had scored at the highest level on every test, had a 98% EVAAS prediction for success, and straight As on his report card. He was also officially classified as Academically Gifted by the school. When a new advanced math class was created, he wasn't invited. When he asked to join, his parents were told no, he needed to be "recommended." School officials told us, with straight faces, that his consistent past success was no indication he could succeed in advanced math, that they were keeping him out for his own good. (This was prior to the NC legislation.) His case was used as an example in the book about math placement, written by the NCSU professors who were working with us, helping to advocate for this and other students.

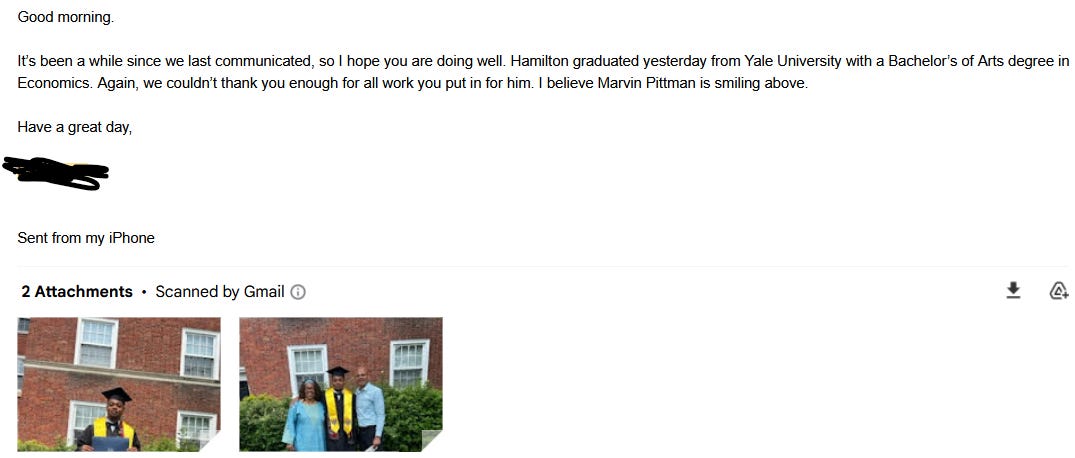
It took advocacy from his church community and our presence to counter the data doublespeak, but we got him in. We, the team from the church, and an NCSU math education professor met monthly with the school staff to check on his progress. We feared they would try to orchestrate his failure to prove their point. In the first meeting, his teacher showed us a graph where he had labeled the x-axis slightly above the line instead of at the point of the arrow. She said this indicated he was not advanced material. We said we would work with him, rather than let them move him out of the class. We kept meeting monthly about his progress. After a few months, instead of showing us evidence of his inability, they were singing his praises and telling us that he was the top scoring student and that he helped others in the class when they were struggling. He stayed in advanced math through graduation. Years later, his parents sent me a photo of him graduating from Yale with an economics degree, thanking us for helping him gain access to this pathway in fifth grade. (Following is the email. The late Marvin Pittman was head of their church’s parent advocacy committee.)

---

A two-tier educational system

The NC math legislation didn't create an equal or fair system. It simply replaced one two-tier system with another. Students with social capital could still access advanced math regardless of their test scores, just as they always had. The difference was that now students without social capital could also earn their way in, but only if they scored at the highest level. While this represented progress by creating an objective pathway for some previously excluded students, it maintained the fundamental inequity where privilege continued to override academic merit for those with advocates, while those without advocates faced a higher bar for entry.

They could have based the legislation on EVAAS predictions, to which every school has access. While understanding how EVAAS works may require specialized statistical knowledge, we routinely rely on complex systems created by experts. Most people don't understand how their smartphones, GPS navigation, or medical imaging equipment work, yet we trust these technologies because they've been validated and proven effective. EVAAS was developed by Dr. William Sanders, a highly respected statistician who earned his Ph.D. in statistics from the University of Tennessee and served as a senior education research manager at SAS Institute, one of the world's leading statistical software companies. His work in educational value-added modeling has been peer-reviewed and widely adopted across multiple states.

Using EVAAS would have provided even more students with the opportunity to learn advanced math concepts, since EVAAS predictions take into account multiple factors beyond just test scores, including teacher quality, student growth trajectories, and other contextual variables. In the schools we worked with, EVAAS had proven remarkably accurate at predicting student success, as demonstrated in the validation data showing 95.9% accuracy predicting success in 8th-grade algebra for students with 70% or higher probability predictions.

The State Board of Education's response to the legislation and the requirement for accountability? They changed the scoring system. They did this in August 2019. (They would not have been able to change the EVAAS predictions.) In their report, they claimed they were trying to better align with national standards, but there was no discussion of how this would affect the legislation's effectiveness. No one addressed the tremendous decline in math scores statewide that resulted from this change. They also altered how scores were reported to schools, combining Level 4 and Level 5 into a single "proficient" category, which meant most schools didn't even notice the dramatic drop in high-achieving students.

A significant advantage of using EVAAS is its stability and objectivity. Unlike test score cut points that the State Board of Education can arbitrarily change, EVAAS uses sophisticated statistical modeling that remains consistent. The Board could theoretically adjust cut scores so that no students score at any proficiency level, but EVAAS would still identify those most likely to succeed in advanced courses. The system is updated annually with new data, making it more responsive and reliable than static test score thresholds. Instead, the legislation relied on this single test score metric, which was more politically palatable but less comprehensive in identifying student potential.

The law was intended to help high school students who excelled in their math classes move into the advanced track. Before the scoring change, 11% of high school students statewide scored at Level 5, the highest level, with some districts seeing rates as high as 25%. The EVAAS Prediction vs. Performance table (above) showed that in 2009, 42,144 students were predicted to be successful in 8th-grade algebra, and only 18,670 students were enrolled. Using EVAAS prediction as the metric would have given 23,474 more students access to advanced math.

After the law passed, which required schools to admit all Level 5 students to advanced classes, and the state changed the scoring scale, fewer than 1,500 (too few to report) high school students in the entire state achieved Level 5.

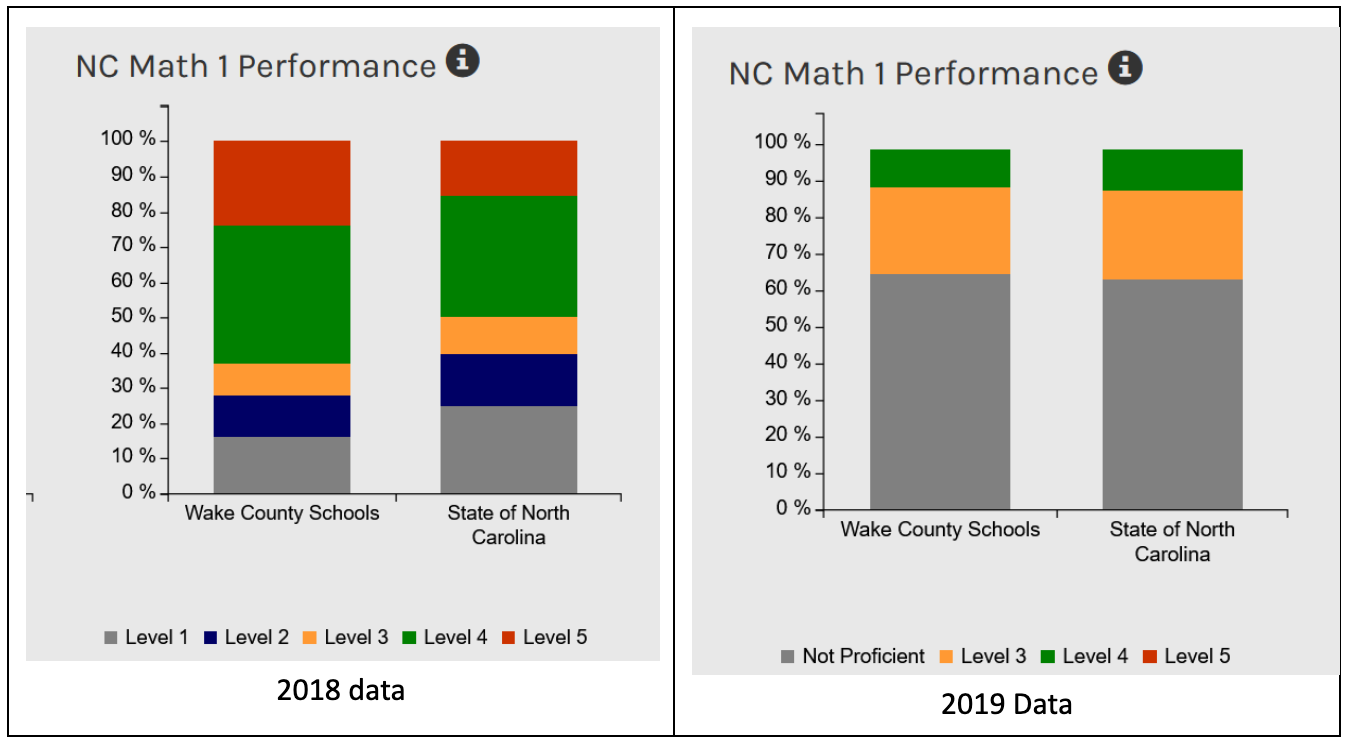
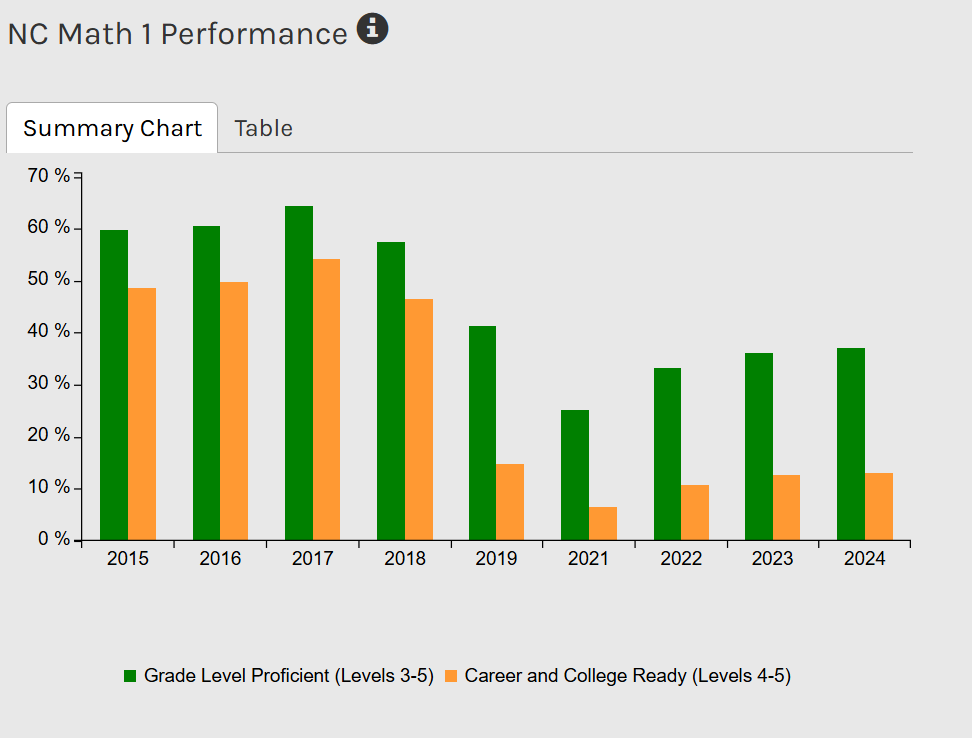
The schools had technically complied with the law while completely subverting its intent. These charts are from the NC School Report Cards.¹⁴ After 2019, the Math 1 Performance charts show no Level 5 and very little Level 4, similar to this.

The following chart shows the State Board's revised reporting format for schools, which combines Level 4 and Level 5 students into a single "Career and College Ready" category for all years shown. Before 2019, these levels were reported separately to schools. Even with the categories combined, you can see the dramatic decline: Level 4-5 performance dropped from around 50% to just 10% after the scoring changes in 2019. The actual Level 5 population—those scoring at the highest level—fell from about 11% of 9th-grade students to too few to report statewide, but this decrease in Level 5 is invisible in the combined reporting. Schools reviewing this data would see a decline but not realize that their highest-achieving students had essentially disappeared.

It's not about lazy teachers or incompetent administrators. It's about a system with enormous inertia that actively resists change, even when that change would help thousands of children.

When educators claim they lack resources for more advanced sections, they're often telling the truth. But this explanation falls apart when higher-scoring students are actively excluded from existing advanced classes while lower-scoring students fill those seats.

---

Expanding the advanced mathematics teaching pipeline

The uncomfortable truth is that fixing the sort would expose the real problem: that we don't have enough teachers capable of teaching advanced mathematics. It's easier to pretend the qualified students don't exist than to admit we can't serve them.

Some states are trying different approaches:

• Texas passed SB 2124, mandating that the top 40% of students be placed in advanced math

• Virginia passed HB 2686, which created multiple pathways into advanced tracks. For example, students who score in the statewide, grade-level upper quartile on the Standards of Learning mathematics assessment must be automatically enrolled in advanced or accelerated mathematics, provided the course is available(§22.1-207.9.A.1). The bill permits parents to opt their child out of automatic enrollment, recognizing parental discretion (§22.1-207.9.A.2). The bill also requires school boards to establish multiple additional pathways for students to enter advanced math. These include:

  • Teacher recommendations

  • Parental recommendations

  • Student preference

  • Demonstrated aptitude through grades, other standardized tests, portfolios, or observations (§22.1-207.9.A.3)

• Indiana, Illinois, and Washington have similar bills under consideration

Perhaps in response to California's legislation,¹⁵ (or maybe it was a coincidence) which required objective measures from 8th-grade algebra for 9th-grade math placement, San Francisco eliminated 8th-grade algebra altogether in the following school year. There was a public outcry that they were eliminating the rigorous math track, probably because that track is known to begin in eighth grade. I have not seen anyone ask whether they eliminated Honors and Advanced Placement math classes. It is possible that some of the 9th-grade algebra classes were taught more rigorously and led to the advanced high school math classes. This would be easy to check. Doing this would subvert the law and maintain the status quo.

Without addressing the fundamental resistance to objective placement criteria, these efforts may meet the same fate as North Carolina's, that is, technical compliance that maintains the inequitable practices these policies were designed to correct. Data-driven placement isn't a panacea, but when properly implemented, it can serve as a tool to reduce the arbitrary decision-making that has historically excluded qualified students from advanced coursework based on demographics rather than academic readiness.

Every year, tens of thousands of students who could excel in advanced mathematics are relegated to standard courses that don't provide the pathway to calculus or Honors and Advanced Placement math in high school.

The solution starts with acknowledging that qualified students exist, admitting we're failing them, and then marshaling the resources to do better. The data is there. The technology exists. What's missing is the will to act.

For those who believe America must cultivate its brightest minds to remain competitive, consider that we're systematically excluding many of our most talented students from advanced mathematics. The fifth grader with a 98% success prediction who needed church advocates to access advanced math? He graduated from Yale with an economics degree. How many others with his ability never got that chance?

When we analyzed the data, we found students in remedial classes who scored higher than their peers in advanced tracks. We are actively holding back high-achieving students who have demonstrated their mathematical ability. In an economy increasingly driven by technical innovation, we're leaving our best mathematical minds to languish in standard courses that don't provide access to the advanced mathematical reasoning and college-preparatory coursework they need to reach their potential.

The crisis in mathematics education extends far beyond 8th-grade algebra placement. The ultimate goal must be ensuring high-achieving students gain access to advanced mathematics and science throughout high school. Any serious accountability effort must track whether students with demonstrated mathematical ability are reaching Honors mathematics, Advanced Placement mathematics, IB mathematics, physics, and chemistry by graduation. North Carolina reported how many students enrolled in Math I/Algebra 1 in middle school, but not how many students enrolled in these advanced STEM courses in high school. For accountability, NC reports the number of students who scored at the highest level in mathematics and then were placed in the most advanced math. They do not report how many students total are in advanced math.

Districts must conduct longitudinal analyses comparing students with similar mathematical abilities. The data may reveal thousands of mathematically gifted students never accessing advanced coursework they've proven capable of mastering. This isn't about advanced math for all; it's about advanced math for students who have already demonstrated advanced ability.

Multiple states have passed legislation forcing schools to allow qualified students to enroll in advanced courses. When laws are necessary to ensure that students scoring at the highest levels can access appropriate mathematics instruction, the system is fundamentally broken.

Parents and policymakers must demand transparency. Can students choose to enroll in advanced courses, or do they need teacher recommendations? How many high-scoring students are excluded from advanced tracks? How many qualified math teachers does the district have? If teacher shortages prevent qualified students from accessing advanced courses, this must be documented and reported publicly. Communities need to know when lack of teachers, not lack of student ability, limits advanced course offerings.

We are wasting mathematical talent on a massive scale. In an era of technological innovation, we deny our brightest students the mathematical foundation they need. Every year represents thousands more students whose STEM pathways are blocked not by ability, but by a system that refuses to recognize their talents.

The data exists. The tools are available. Ask the hard questions. Demand transparency. Document the barriers. Don't accept explanations that high-achieving students are being excluded "for their own good." Their futures depend on getting this right.

Editor’s note: This story previously contained an example of a story from a universal screening program in Broward County, Florida reported in the New York Times and Washington Post as having led to a sharp increase in Black and Hispanic enrollment in gifted programs. While universal screening is laudable, the news articles omitted that the program admitted English language learners and free-or-reduced price lunch students at a lower threshold than others, adding complexity that makes the story awkwardly suited to a passing reference. The Broward County story remains worth understanding, and you can read the original study here. Thanks to 3rdMoment for bringing the details to our attention.

---

Janet Johnson is the President of Edstar Analytics, a North Carolina-based research firm specializing in the evaluation of K-12 education programs. She holds a Ph.D. in Mathematics Education with a minor in Statistics from NC State University. Dr. Johnson has led major federally funded research and evaluation projects focused on mathematics placement, STEM education, dropout prevention, and college readiness. Her work has helped school systems across the country use data to identify and support high-achieving students, ensuring they are placed in appropriately rigorous academic pathways.

John Wittle serves as the Chief Technology Officer at Edstar Analytics, where he designs and maintains secure data systems used in large-scale evaluations of K-12 educational initiatives. With a background in systems administration and certification from the Linux Foundation, he has created tools that support school counselors, collect sensitive data for education programs, and deliver online professional development. John ensures that Edstar’s technology infrastructure meets the standards for cybersecurity and performance, helping transform educational data into actionable insights for schools and policymakers.

1. SAS Institute (2009b). “Mathematics Talent Identification and Reclamation in Moore County School District.” Raleigh, NC.

2. Haynie, Glenda. (2009). “Middle School Algebra I: Effective Instructional Strategies with Comparison to High School Practices.” WCPSS Evaluation & Research Department.

3. SAS Institute. (2009a). “Identifying students who are ready for Algebra I: Algebra readiness curriculum supplement.” Raleigh, NC.

4. See SAS Institute (2009b).

5. General Assembly of North Carolina, 2015.

6. Stiff, L. V., Johnson, J. L., & Akos, P. (2011). “Examining what we know for sure: Tracking in middle grades mathematics.” In W. F. Tate, K. D. King, & C. R. Anderson (Eds.), Disrupting tradition: Research and practice pathways in mathematics education, 63–75. Reston, VA: National Council of Teachers of Mathematics, Inc.

7. Stiff, L. V., & Johnson, J. L. (2011). “Mathematical reasoning and sense making begins with the opportunity to learn.” In M. E. Strutchens & J. R. Quander (Eds.), Focus in high school mathematics: Fostering reasoning and sense making for all students, 85-100. National Council of Teachers of Mathematics.

8. McGrath, D. J., & Kuriloff, P. J. (1999). “They’re going to tear the doors off this place: Upper-middle-class parent school involvement and the educational opportunities of other people’s children.” Educational Policy, 13(5), 603–629.

9. Vanfossen, B. E., Jones, J. D., & Spade, J. Z. (1987). “Curriculum tracking and status maintenance.” Sociology of Education, 60(2), 104–122.

10. Oakes, J. (1993). “Ability grouping, tracking, and within-school segregation in the San Jose Unified School District.” Los Angeles: UCLA.

11. Stone, C. B. (1998). “Leveling the playing field: An urban school system examines equity in access to mathematics curriculum.” The Urban Review, 30. 295-307.

12. O’Connor, C., Lewis, A., & Mueller, J. (2007). “Researching ‘Black’ educational experiences and outcomes: Theoretical and methodological considerations.” Educational Researcher 36(9), 541–552.

13. Stiff, L. V., Johnson, J. L., & Akos, P. (2011).

14. See https://ncreports.ondemand.sas.com/src/.

15. The 2014 Senate Bill 359, Chapter 508.